二次根式的定义
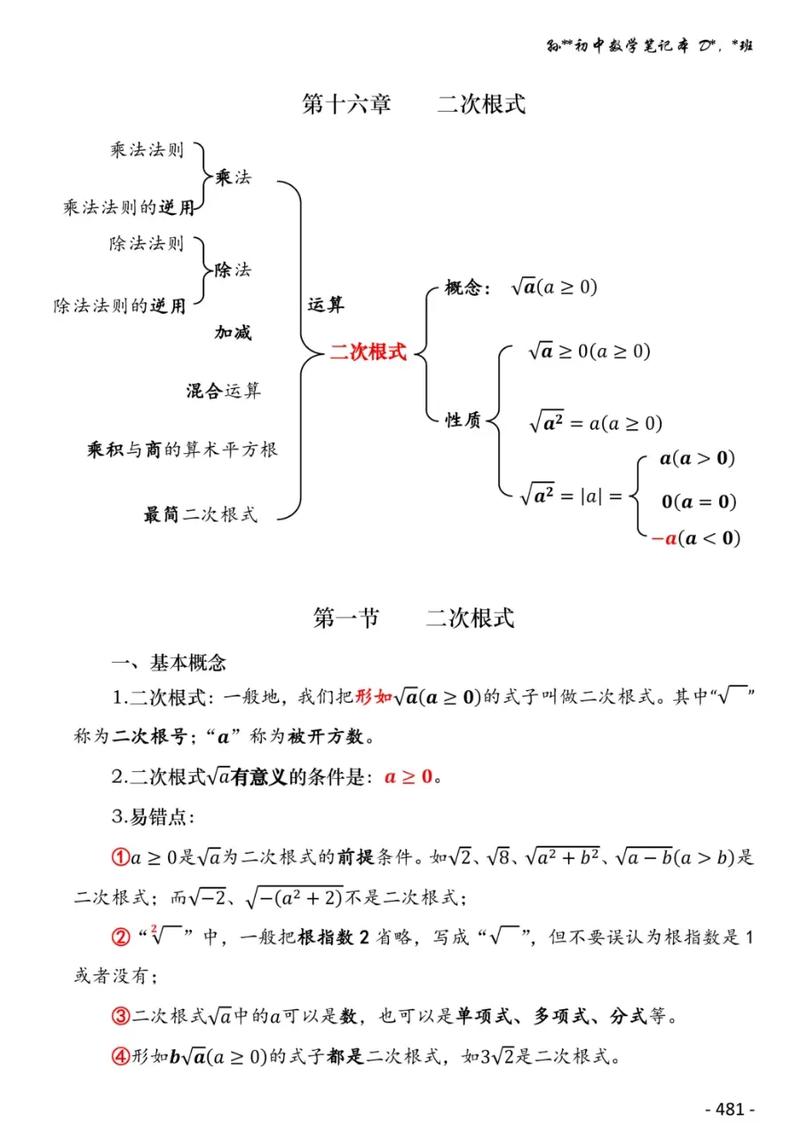
二次根式指的是形如 $\sqrt{a}$ 的表达式,$a$ 是一个非负数(即 $a \geq 0$),这里的 $\sqrt{}$ 表示平方根,$\sqrt{a}$ 可以理解为 $a$ 的平方根。
(图片来源网络,侵删)
- 定义:形如 $\sqrt{a}$ 的表达式,$a \geq 0$,称为二次根式。
- 平方根的定义:平方根是指一个数的平方等于另一个数的数,记作 $\sqrt{a}$,即 $\sqrt{a} = b$,$b^2 = a$。
- 根号的种类:二次根式只涉及平方根,即 $\sqrt{}$。
二次根式的性质
二次根式的性质是确定其行为的基础,包括定义域、非负性、运算规则等。
- 定义域:二次根式的被开方数 $a$ 必须是非负数,即 $a \geq 0$。
- 非负性:$\sqrt{a} \geq 0$,无论 $a$ 是正数还是零。
- 平方根的性质:
- $\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}$(当 $a, b \geq 0$ 时)。
- $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$(当 $a \geq 0$,且 $b > 0$ 时)。
- $\sqrt{a^n} = a^{n/2}$(当 $a \geq 0$ 且 $n$ 为偶数时)。
- 根号的运算规则:
- 加法:$\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}$(除非 $a$ 和 $b$ 为零)。
- 减法:$\sqrt{a} - \sqrt{b} \neq \sqrt{a - b}$(除非 $a$ 和 $b$ 为零)。
- 乘法:$\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}$(当 $a, b \geq 0$ 时)。
- 除法:$\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$(当 $a \geq 0$,且 $b > 0$ 时)。
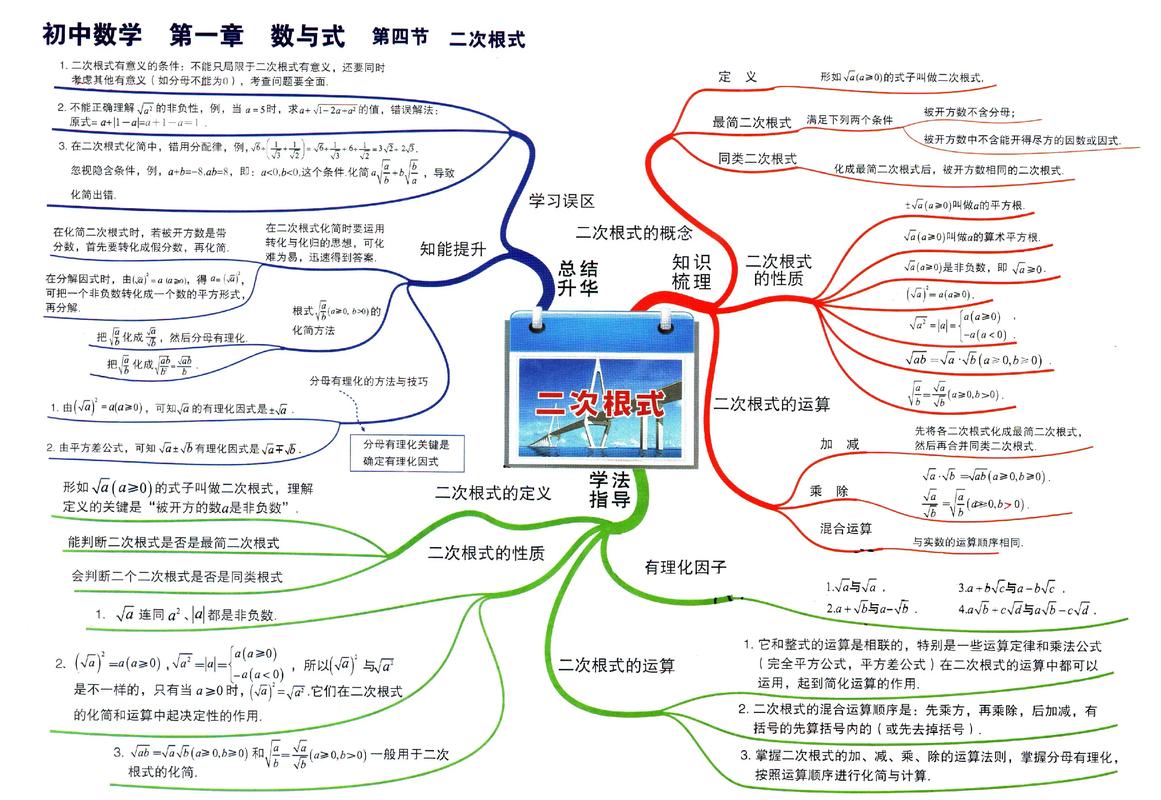
二次根式的化简
化简二次根式是为了将其表示为最简形式,便于后续的运算和比较。
(图片来源网络,侵删)
- 最简二次根式的定义:一个二次根式,如果其被开方数不含平方因子(即不含有平方数或平方数的乘积),则称为最简二次根式。
- 化简步骤:
- 将系数和被开方数分别分解质因数。
- 将被开方数中的平方因子和平方数因子提取出来,作为根号的因数。
- 将提取出的平方因子或平方数因子作为根号的系数,将剩下的作为新的被开方数。
例子:
- $\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}$。
- $\sqrt{5} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}$。
- $\sqrt{\frac{49}{2}} = \frac{\sqrt{49}}{\sqrt{2}} = \frac{7}{\sqrt{2}}$,进一步化简为 $\frac{7\sqrt{2}}{2}$。
二次根式的实际应用
二次根式在实际生活中有许多应用,特别是在几何、物理和工程等学科中。
-
几何中的应用:
- 勾股定理:在直角三角形中,斜边的平方等于两条直角边的平方和,即 $c^2 = a^2 + b^2$,斜边 $c$ 可以表示为 $c = \sqrt{a^2 + b^2}$。
- 面积计算:在计算某些几何图形的面积时,二次根式也会出现,正方形的边长为 $a$,则面积为 $a^2$,其平方根即为边长。
-
代数中的应用:
- 方程求解:在解二次方程时,有时需要对二次根式进行化简或运算,解方程 $x^2 = 5$ 时,解为 $x = \sqrt{5}$ 或 $x = -\sqrt{5}$。
- 物理中的应用:在力学和能量计算中,二次根式也会出现,动能公式为 $E = \frac{1}{2}mv^2$,$v$ 是速度,$m$ 是质量,动能的平方根 $\sqrt{E}$ 可以表示为 $v = \sqrt{\frac{2E}{m}}$。
二次根式的不同类型
二次根式也可以根据其根号内的被开方数的不同,分为以下几种类型:
-
完全平方根:
- 被开方数是一个完全平方数或平方数的倍数。
- $\sqrt{9} = 3$,$\sqrt{16} = 4$,$\sqrt{18} = 3\sqrt{2}$。
-
开平方根:
- 被开方数是一个完全平方数。
- $\sqrt{16} = 4$,$\sqrt{25} = 5$,$\sqrt{36} = 6$。
-
最简二次根式:
- 被开方数不含平方因子。
- $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$。
-
带分数根式:
- 被开方数中包含分数,但整体是一个最简二次根式。
- $\sqrt{\frac{1}{4}} = \frac{1}{2}$,$\sqrt{\frac{9}{4}} = \frac{3}{2}$。
二次根式是一个重要的数学概念,其定义、性质、化简方法以及实际应用在各个学科中都有广泛的应用,通过系统地梳理二次根式的知识网络框架,可以帮助读者更好地理解和掌握这一知识点。